Scorpion

KPA/COA 8 rotor machine 密码算法： p=plain,c=cipher,f=offsetenc:c=e[p+f] mod 96dec:p+f=d[c] mod 96其中数组e[]和d[]分别为用于加密和解密的数组p = plain, c = cipher, f = offset \\ enc: c = e[p+f] \ mod \ 96 \\ dec: p+f = d[c] \ mod \ 96 \\ 其中数组e[]和d[]分别为用于加密和解密的数组 p=plain,c=cipher,f=offsetenc:c=e[p+f] mod 96dec:p+f=d[c] mod 96其中数组e[]和d[]分别为用于加密和解密的数组 KPA（known plaintext attack） 已知明文攻击定义：已知部分明文和对应的密文，从而破解出对应的密钥和加密算法。 但是这里已知加解密算法以及一定包含正确密钥的字典。因此只需要依次尝试密钥然后判断是否正确即可。 用Java实现如下： 定义一个public static void kpa(String plain, Str ...

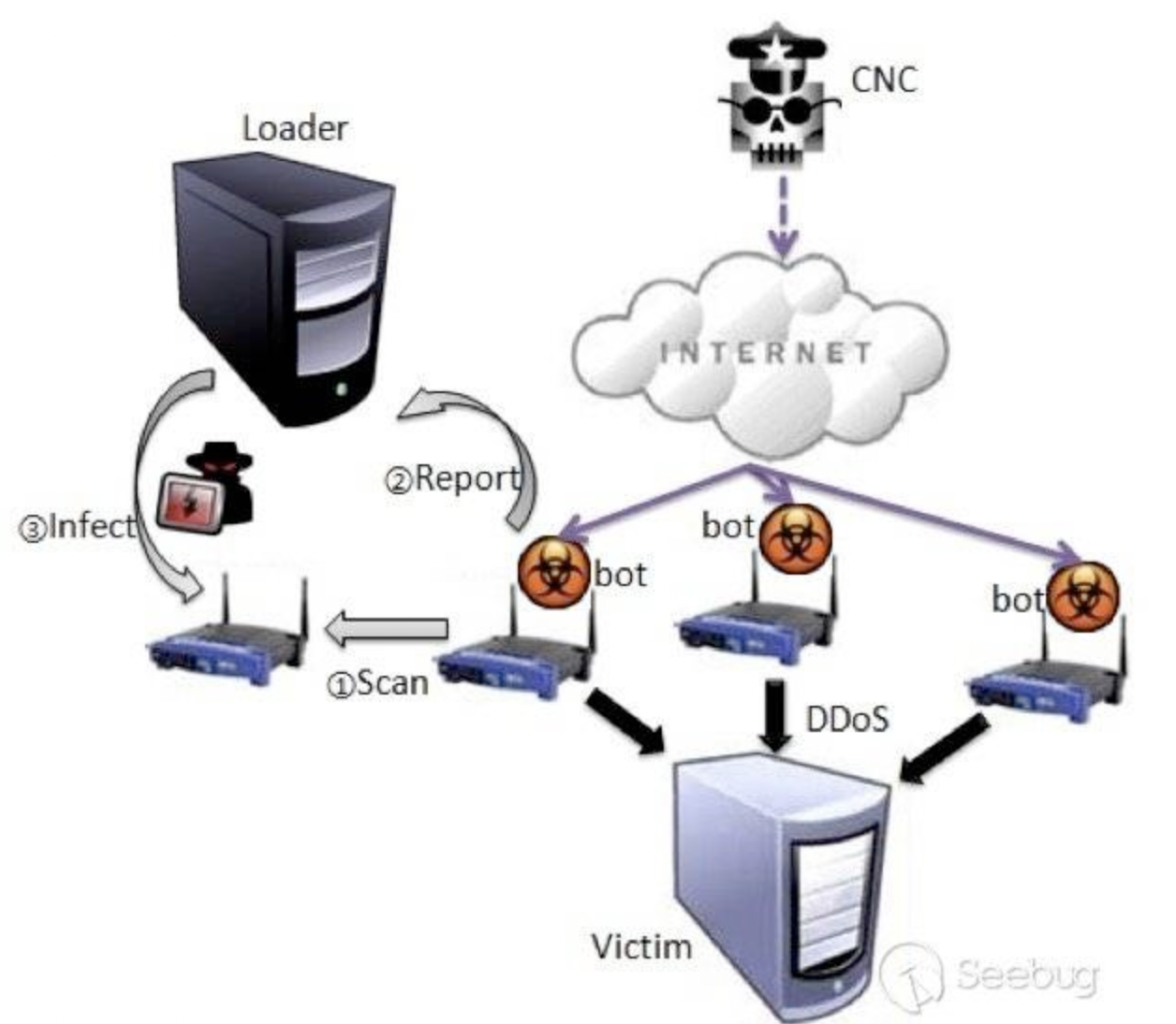
Mirai源码分析 大概看了下整体结构和流程，然后细看了一下加解密部分。 代码结构： 123456loader/src 将payload上传到受感染的设备mirai/bot 在受感染设备上运行的恶意payloadmirai/cnc 恶意者进行控制和管理的接口mirai/tools 提供的一些工具其中，cnc部分是Go语言编写的，余下都是C语言 整体网络拓扑关系如下图所示，受感染的设备扫描其他可能受感染的设备，扫描到之后就讲设备信息等提供给loader，loader将payload下载到可能受感染的设备上，比如宏病毒，js下载者等。被感染的设备与c2服务器连接，并向特定受害者发起ddos攻击。 loader 主要功能是向感染设备上传（wget、tftp、echo方式）对应架构的payload文件 目录结构 1234567headers/ 头文件目录binary.c 将bins目录下的文件读取到内存中，以echo方式上传payload文件时用到connection.c 判断loader和感染设备telnet交互过程中的状态信息main.c ...

交叉编译 环境 Ubuntu 20 crypto++ 8.8 g+±arm-linux-gnueabi 9 (.4.0 安装依赖 交叉编译工具链 12sudo apt updatesudo apt-get install g++-arm-linux-gnueabi gcc-arm-linux-gnueabi 密码库 1git clone <https://github.com/weidai11/cryptopp.git> 设定环境 编辑TestScripts中的setenv-embedded.sh 1ARM_EMBEDDED_CXXFLAGS="-|/usr/arm-linux-gnueabi/include/c++/9 -|/usr/arm-linux-gnueabi/include/c++/9/arm-linux-gnueabi" 主要需要改版本，根据路径查看 编译 123sudo make -f GNUmakefile-crosssudo make -f GNUmakefile-cross static static dynamic crypte ...

野人与传教士 用遍历方法寻找所有可能路径，因此用DFS比较合适，因此BFS虽然能找到目标状态，但是要找到目标状态的前一路径比较困难） 设定状态表示，虽然可以直接用（M，C，b）三元组分别表示左岸传教士，野人数量以及船是否在左岸。实现时为了方便还是定义一个class类state分别表示 1234567class State: def __init__(self,lm,rm,lc,rc,ship): self.lm = lm self.rm = rm self.lc = lc self.rc = rc self.ship = ship 因此初始状态init为 1init = State(M,0,C,0,1) 定义一个函数判断是否为目标状态 12345def is_goal(state): if state.lm == 0 and state.lc == 0 and state.rm == M and state.rc == C: return 1 return 0 能实施的操作用o ...

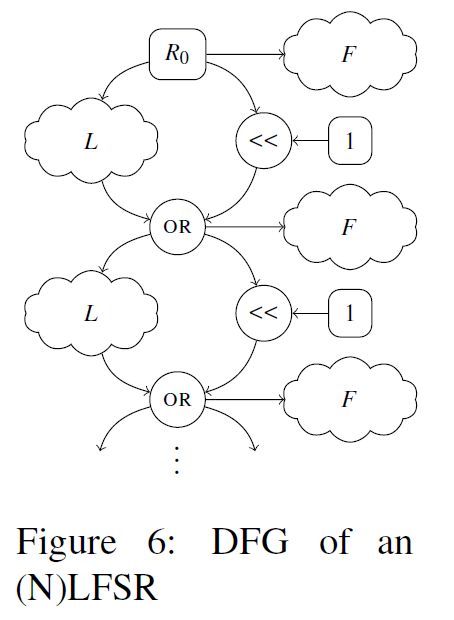
lfsr 算法 假设R为一个（N）LFSR，对于每一轮，使用反馈函数L从R中的比特位（子集）生成一个新的比特位。如果L是线性的，例如异或，我们把R称为一个LFSR。反之，如果L是非线性的，R就是一个NLFSR。寄存器R中的所有位都向左移动一个位置，忽略最高位，新产生的位被放在最低位且被输出。 所以 对每轮i∈[0, 1, ..., n]Ri+1=(Ri<<1) xor L(Ri)outputi=(Ri)对每轮i\in[0,\ 1,\ ...,\ n ] \\ R_{i+1} = (R_i << 1)\ xor\ L(R_i) \\ output_i = (R_i) 对每轮i∈[0, 1, ..., n]Ri+1​=(Ri​<<1) xor L(Ri​)outputi​=(Ri​) signature TRANSIENT用于表示从表达式生成的DFG节点不是很重要，图清除过程中可以简化。 OPAQUE中 o1为clamp-label（可选）：为节点类型命名。与任何其他类型的节点进行比较都为真，并增加了所有带有相同类型标签的 opaque 必须映射到相 ...

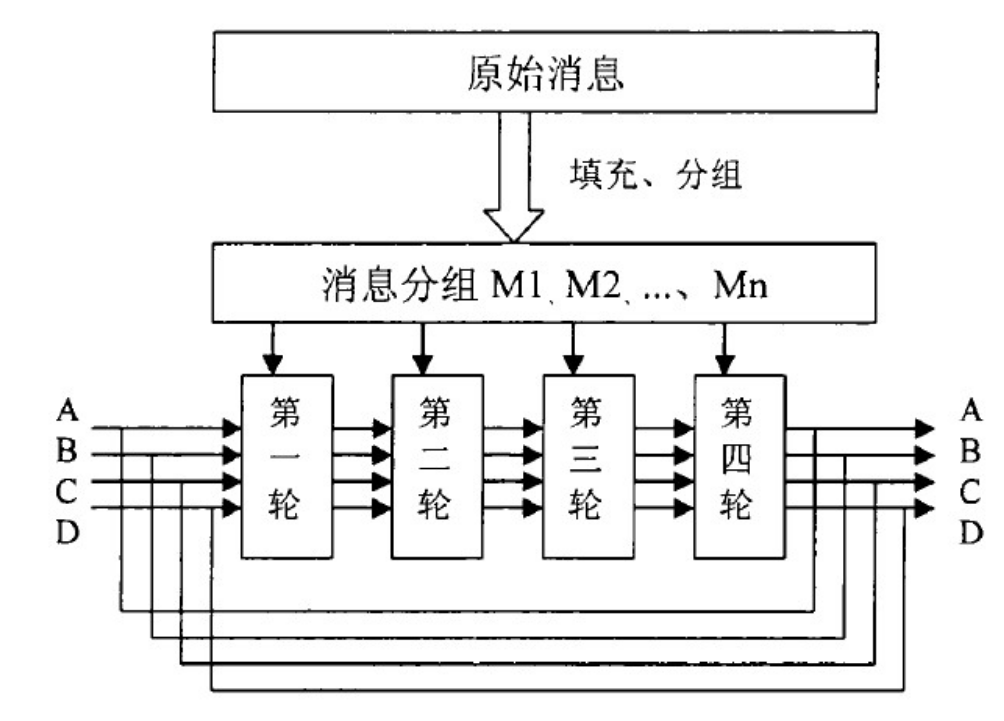
sha1 与md5类似，差异用标注 算法 输入：任意长的消息，512 比特长的分组。原始报文长度不能超过2的64次方 输出：160 比特的消息摘要 整体流程如下： 首先填充原始消息使得对512求余的结果等于448，然后64位记录其长度。 512bit一组分为n组。每组中32bit为一段，分为16段 将上述16段扩充到80段 对每一组，循环4轮运算，得到新的A,B,C,D,E作为下一组的初始值 最后得到的A,B,C,D,E加上第n组原来A,B,C,D,E的值（即计算前的值） 按照地址的顺序从低到高打印对应的A,B,C,D,E值，就是所求的sha1值。 填充 如果输入信息的长度(bit)对512求余的结果不等于448，就需要填充使得对512求余的结果等于448。填充的方法是填充一个1和n个0。填充完后，信息的长度就为N*512+448(bit)。 然后用64位来存储填充前信息长度。这64位加在第一步结果的后面，这样信息长度就变为N*512+448+64=(N+1)*512位 比如，需要加密消息"gnubd"，最后被填充为 小端字节序存储 123467 6E 75 ...

DFG论文 Lestringant,P., Guihéry,F. and Fouque,P… Automated identification of cryptographic primitives in binary code with data flow graph isomorphism. (2015)In Proceedings of the 10th ACM Symposium on Information, Computer and Communications Security, pages 203–214. 背景 软件用密码算法保护通信安全性以及数据安全。但算法的选择，具体实现方法，输入参数的生成对数据安全性有巨大影响。所以分析有密码的二进制文件安全性时，需要确保没有上述几点影响系统安全。所以首先需要识别并定位密码算法。但分析是耗时费力的，所以需要自动化工具 现有方法： 静态分析主要根据常量或I/O关系，大多利用统计特性，可能不准确 动态分析性能不太好 缺陷： 手动构建签名的准确性 依赖启发式代码片段选择 仅限于已知密码原语 constant state 特色 ...

MD5 算法 输入：任意长的消息，512 比特长的分组。 输出：128 比特的消息摘要 整体流程如下： 首先填充原始消息使得对512求余的结果等于448，然后64位记录其长度。 512bit一组分为n组。每组中32bit为一段，分为16段 对每一组，循环4次下述4轮运算，得到新的A,B,C,D作为下一组的初始值 最后得到的A,B,C,D加上第n组原来A,B,C,D的值（即计算前的值） 按照地址的顺序从低到高打印对应的A,B,C,D值，就是所求的MD5值。 填充 如果输入信息的长度(bit)对512求余的结果不等于448，就需要填充使得对512求余的结果等于448。填充的方法是填充一个1和n个0。填充完后，信息的长度就为N*512+448(bit)。 然后用64位来存储填充前信息长度。这64位加在第一步结果的后面，这样信息长度就变为N*512+448+64=(N+1)*512位 比如，需要加密消息"gnubd"，最后被填充为 小端字节序存储 123467 6E 75 62 64 80 00 00 00 00 00 00 00 00 00 ...

[ichunqiu-crypto]writeup [phrackCTF]BrokenPic 题面：这里有个图片，可是好像打不开？ 给出一个bmp图片 RSA [IceCTF]Round Rabins【Cipolla】 发现n能开平方，提示rabin，e应为2，所以转化为下式求m的值 c=m2(mod p2)c = m^2 (mod\ p^2) c=m2(mod p2) 先利用Cipolla算法求得r，使得（本题中k为2） a=r2(mod p)所以(r2−a)k=0(mod pk)二项式分解(r2−a)k=t2−u2a=0(mod pk)t2u−2=a=x2(mod pk)所以x=t∗u−1(modpk)即最后所求ma = r^2 (mod\ p) \\所以 (r^2-a)^k = 0 (mod\ p^k) \\二项式分解 (r^2-a)^k=t^2-u^2a=0(mod\ p^k) \\t^2u^{-2} = a = x^2(mod\ p^k) \\所以 x = t*u^{-1} (mod p^k) \\即最后所求m a=r2(mod p)所以(r2−a)k=0(mod pk)二项式 ...

[BUUCTF-crypto]writeup 数学 [WUSTCTF2020]大数计算 Note：理解问题，题目说要十六进制，前8位不知道是取十进制的前八位然后转换还是取十六进制的前八位，所以（错误就得多试试 1234567a = math.factorial(2020)print(a)print(hex(int(str(a)[:8])))x = pow(520,1314) + pow(2333,666)print(x)print(hex(int(str(x)[:8]))) 宇宙终极问题：x³＋y³＋z³＝42 (-80538738812075974)³ + 80435758145817515³ + 12602123297335631³ = 42 part-4，简单的积分，计算面积即可，再加36得520 编码 鸡藤椒盐味 【汉明码】 设将要进行检测的二进制代码为n位，为使其具有纠错能力，需要再加上k位的检测位，组成n+k位的代码。那么，新增加的检测位数k应满足： 2k≥n+k+1或2k-1≥n+k 古典 [INSHack2018]Crypt0r part 1【tcp流+简单替换】 ...