KPA/COA

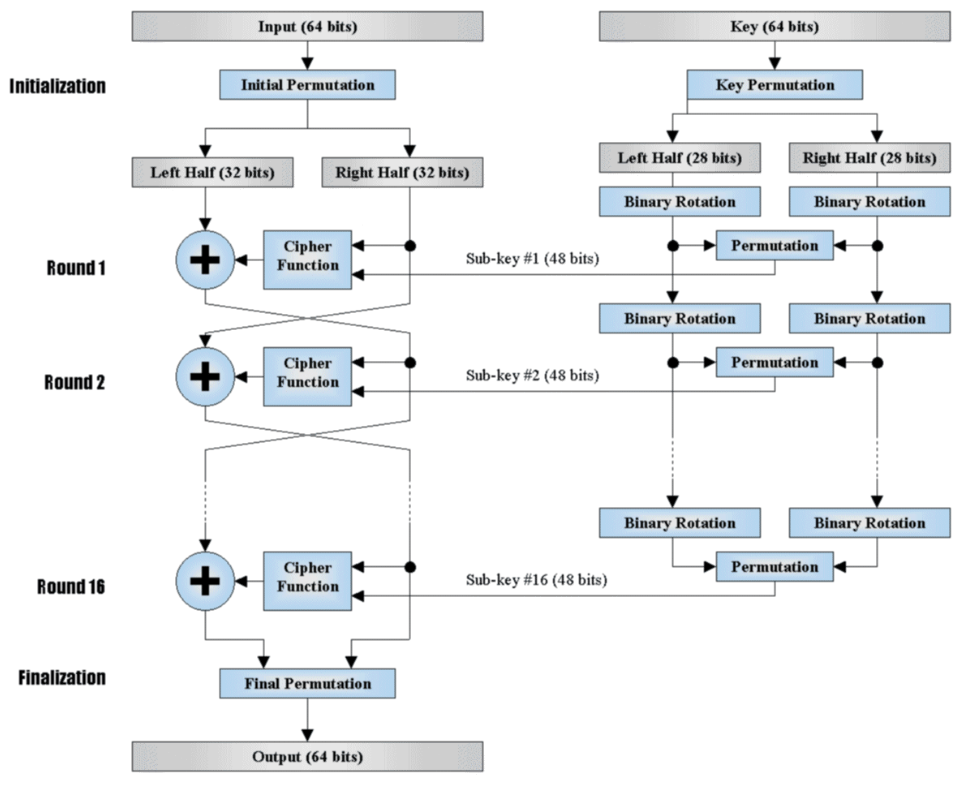
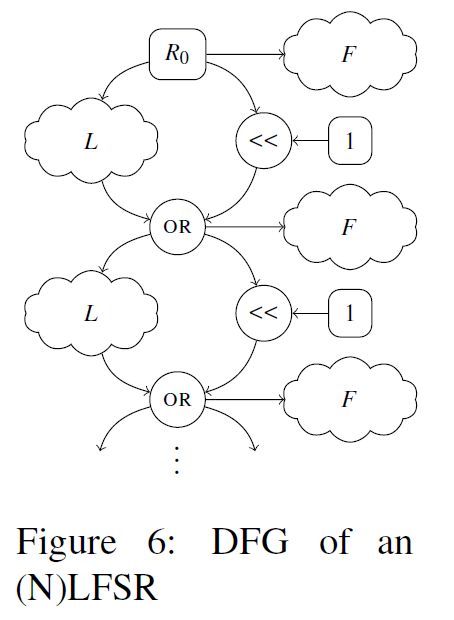
8 rotor machine

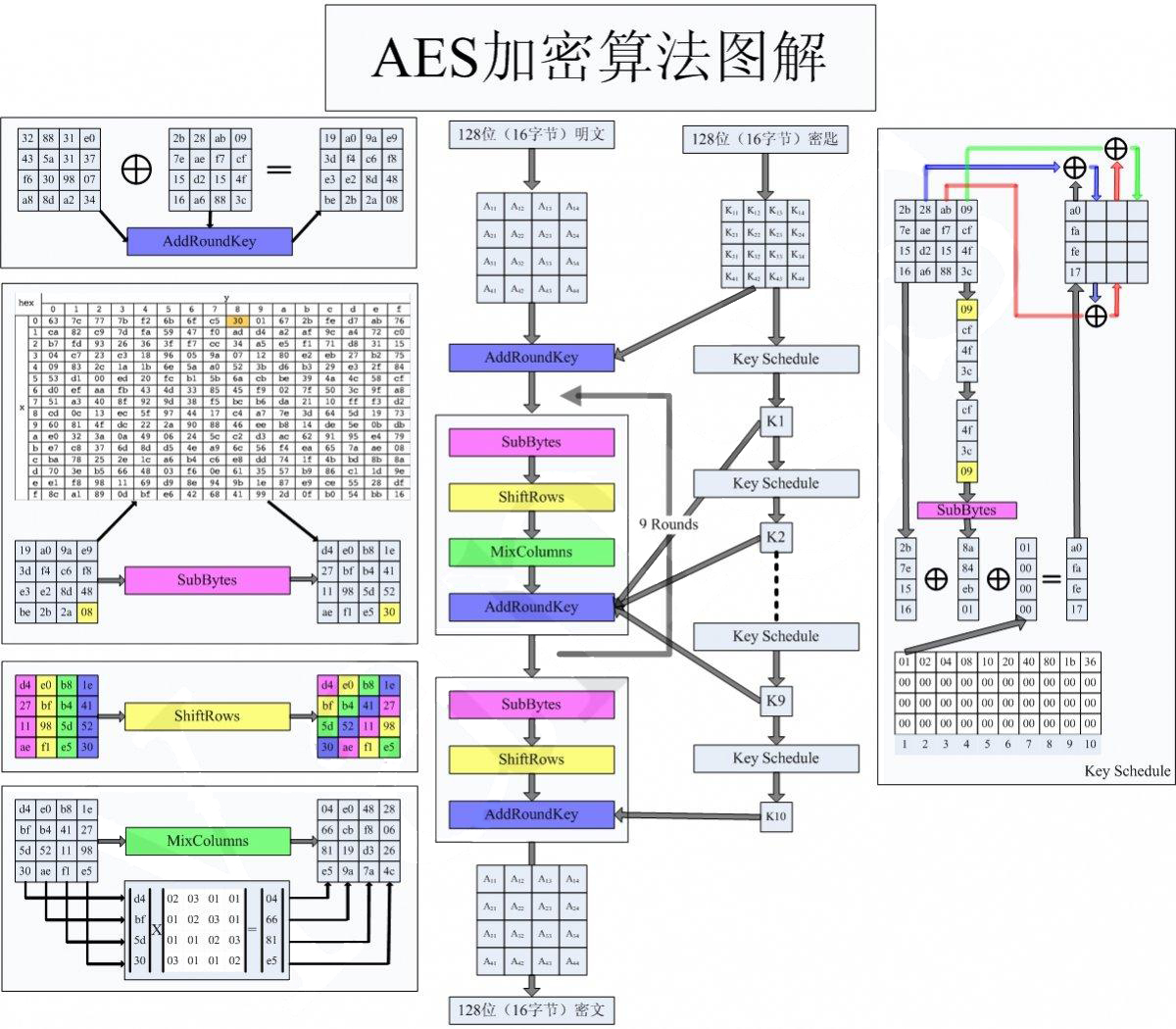
密码算法：

$p = plain, c = cipher, f = offset \\ enc: c = e[p+f] \ mod \ 96 \\ dec: p+f = d[c] \ mod \ 96 \\ 其中数组e[]和d[]分别为用于加密和解密的数组$

KPA（known plaintext attack）

已知明文攻击定义：已知部分明文和对应的密文，从而破解出对应的密钥和加密算法。

但是这里已知加解密算法以及一定包含正确密钥的字典。因此只需要依次尝试密钥然后判断是否正确即可。

用Java实现如下：

定义一个public static void kpa(String plain, String ciphertext, String keyfile)函数，参数分别为已知的部分明文plain，密文ciphertext，密码字典文件名keyfile。

// main函数中写入具体信息，然后调用该函数
public static void main(String[] args) throws IOException {

  String ciphertext = "***"; // ciphertext
  String plaintext = "Th";  // first two letters

  kpa(plaintext,ciphertext, "passwords");
}

kpa函数主要功能：

读取passwords文件

public static void kpa(String plain, String ciphertext, String keyfile) throws IOException {
  FileInputStream passwords = new FileInputStream(keyfile);
  try (BufferedReader bufferedReader = new BufferedReader(new InputStreamReader(passwords))) {
    String password;
    while((password = bufferedReader.readLine()) != null) {
      String plaintext = encdec(2,password,ciphertext);
      if(plaintext.startsWith(plain)) {
        System.out.printf("key: %s , plaintext: %s\n",password,plaintext);
      }
    }
  }
}

调用解密函数，得到明文并判断前两个字符是否为‘Th’，是则输出，否则继续判断下一个密钥解密出的明文：

while((password = bufferedReader.readLine()) != null) {
  String plaintext = encdec(2,password,ciphertext);
  if(plaintext.startsWith(plain)) {
    System.out.printf("key: %s , plaintext: %s\n",password,plaintext);
  }

最后共得到4个可能的结果。已知明文是具有意义的英文句子，很明显只有一个满足。

因此密钥为chilli

COA(ciphertext only attack)

唯密文攻击：在只知道密文的情况下，求解明文或密钥

但是这里已知加解密算法以及一定包含正确密钥的字典。那么关键在于如何确定解密后的明文是否为有意义的英文句子。其余读取密钥并解密等和上述一样，这里主要说明判断明文是否有意义的方法，主要有以下三种：

首字母为大写

1	Character.isUpperCase(plaintext.charAt(0))

单词必须有效，即不包含数字；连字符不在单词开头或结尾，并且连字符前面和后面一个均为字母，且最多只有一个连字符；符号‘！’，‘.’ ，','不是在单词末尾。

public static boolean isWord(String word) {
    int n = word.length();
    boolean hasHyphens = false;
    for (int i = 0; i < n; i++) {
        if (Character.isDigit(word.charAt(i))) {
            return false;
        } else if (word.charAt(i) == '-') {
            if (hasHyphens || i == 0 || i == n - 1 || !Character.isLetter(word.charAt(i - 1)) || !Character.isLetter(word.charAt(i + 1))) {
                return false;
            }
            hasHyphens = true;
        } else if (word.charAt(i) == '!' || word.charAt(i) == '.' || word.charAt(i) == ',') {
            if (i != n - 1) {
                return false;
            }
        }
    }
    return true;
}

用正则表达式进行判断，排除一些无意义字符。

1
2
3

public static boolean isValid(String sentence) {
    return sentence.matches("^[a-zA-Z0-9 ():.!?-]*");
}

最后只输出一个结果，也可以很明显看到是有意义的英文字符。密钥为molly

Unicity distance

根据信息论

$已知密码算法的字符集数量L = 96，但是有意义的英文句子组成为26，那么R = log2(26) = 4.7 \\ 假设句子有N个字符，那么可能的数量为L^N = (2^R)^N (L = 2^R) \\ 有意义$

有意义

The number of meaningful messages can be expressed in terms of the rate for the language is

$2^rN.$

If we assume that all messages are equally likely, then the probability of getting a meaningful message by chance is

$number \ of \ apprently \ meaningful \ message / number \ of \ possible \ message \\ = 2^{rN} / 2^{RN} = 2^{(r-R)*N} = 2^{-DN}$

已知密钥数量集K=9473，那么错误的数量为9472

The expected number of false solution that look like they might be right = number of wrong keys * probability of chance meaningful message $= 9472 * 2^-DN$

We can define the value of N at the crossover point when the exponent = 0 as the unicity distance

$\\ log2(9472) - D*Nu = 0 \\ R = log2(26) = 4.7 \\ 英文中r一般取1.5 \\ D = R - r = 3.2 \\ Nu = log2(9472) / D = 4.127954176759047$

因此理论上至少需要5个字符

但是实际上还和判断句子是否为有意义的英文句子的判断方法有关。

差异主要在于判断解密出来的明文是否为有意义的英文句子的方法；以及是否需要人工辅助，如果人工辅助那么确实即使只有5个字符，即使输出所有可能明文，那么也可以判断，只是实际上这样过于耗时费力。